Portal:Mathematics

The Mathematics Portal

Pythagoras

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 

  

  The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

  
  
  In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
  $$\sum _{n=1}^{m}n(-1)^{n-1}.$$
  
  The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
  $$1-2+3-4+\cdots ={\frac {1}{4}}.$$ (Full article...)
• 

  

  The weighing pans of this balance scale contain zero objects, divided into two equal groups.

  
  In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if y is even then y + x has the same parity as x—indeed, 0 + x and x always have the same parity.
  
  Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
• 
  
  

  

  Archimedes Thoughtful
  by Domenico Fetti (1620)

  
  Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
  
  Archimedes' other mathematical achievements include deriving an approximation of pi, defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 

  

  High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

  
  
  General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
  
  By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
• 
  
  

  

  Portrait by Jakob Emanuel Handmann, 1753

  
  Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleːɔnhart ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician, and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.
  
  Euler is regarded as one of the greatest, most prolific mathematicians in history and the greatest of the 18th century. Several great mathematicians who produced their work after Euler's death have recognised his importance in the field as shown by quotes attributed to many of them: Pierre-Simon Laplace expressed Euler's influence on mathematics by stating, "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." His 866 publications and his correspondence are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quartos. He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia. (Full article...)
• 
  In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
  
  Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  In mathematics, a group is a set with an operation that associates an element of the set to every pair of elements of the set (as does every binary operation) and satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 
  
  

  

  Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

  
  An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.
  
  While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a reclusive primitive lifestyle.
  
  Kaczynski murdered three people and injured 23 others between 1978 and 1995 in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating a nature-centered form of anarchism. (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor; German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, whilst Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 

  

  
  Émile Michel Hyacinthe Lemoine (French: [emil ləmwan]; 22 November 1840 – 21 February 1912) was a French civil engineer and a mathematician, a geometer in particular. He was educated at a variety of institutions, including the Prytanée National Militaire and, most notably, the École Polytechnique. Lemoine taught as a private tutor for a short period after his graduation from the latter school.
  
  Lemoine is best known for his proof of the existence of the Lemoine point (or the symmedian point) of a triangle. Other mathematical work includes a system he called Géométrographie and a method which related algebraic expressions to geometric objects. He has been called a co-founder of modern triangle geometry, as many of its characteristics are present in his work. (Full article...)

Selected image –

animation of the classic "butterfly-shaped" Lorenz attractor seen from three different perspectives

Lorenz attractor

Credit: Wikimol

The Lorenz attractor is an iconic example of a strange attractor in chaos theory. This three-dimensional fractal structure, resembling a butterfly or figure eight, reflects the long-term behavior of solutions to the Lorenz system, a set of three differential equations used by mathematician and meteorologist Edward N. Lorenz as a simple description of fluid circulation in a shallow layer (of liquid or gas) uniformly heated from below and cooled from above. To be more specific, the figure is set in a three-dimensional coordinate system whose axes measure the rate of convection in the layer (x), the horizontal temperature variation (y), and the vertical temperature variation (z). As these quantities change over time, a path is traced out within the coordinate system reflecting a particular solution to the differential equations. Lorenz's analysis revealed that while all solutions are completely deterministic, some choices of input parameters and initial conditions result in solutions showing complex, non-repeating patterns that are highly dependent on the exact values chosen. As stated by Lorenz in his 1963 paper Deterministic Nonperiodic Flow: "Two states differing by imperceptible amounts may eventually evolve into two considerably different states". He later coined the term "butterfly effect" to describe the phenomenon. One implication is that computing such chaotic solutions to the Lorenz system (i.e., with a computer program) to arbitrary precision is not possible, as any real-world computer will have a limitation on the precision with which it can represent numerical values. The particular solution plotted in this animation is based on the parameter values used by Lorenz (σ = 10, ρ = 28, and β = 8/3, constants reflecting certain physical attributes of the fluid). Note that the animation repeatedly shows one solution plotted over a specific period of time; as previously mentioned, the true solution never exactly retraces itself. Not all solutions are chaotic, however. Some choices of parameter values result in solutions that tend toward equilibrium at a fixed point (as seen, for example, in this image). Initially developed to describe atmospheric convection, the Lorenz equations also arise in simplified models for lasers, electrical generators and motors, and chemical reactions.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 
  Donkey Kong Jr. Math is an edutainment platform video game developed and published by Nintendo for the Nintendo Entertainment System. It is a spin-off of the 1982 arcade game Donkey Kong Jr. In the game, players control Donkey Kong Jr. as he solves math problems set up by his father Donkey Kong. It was released in Japan in 1983 for the Family Computer, and in North America and the PAL region in 1986.
  
  It is the only game in the Education Series of NES games in North America, owing to the game's lack of success. It was made available in various forms, including in the 2002 GameCube video game Animal Crossing and on the Virtual Console services for Wii and Wii U in 2007 and 2014 respectively, and in 2024 for the Nintendo Switch Online service. Donkey Kong Jr. Math was a critical and commercial failure. It has received criticism from several publications including IGN staff, who called it one of the worst Virtual Console games. (Full article...)
• 

  

  Schematic representation of the Dirac delta function by a line surmounted by an arrow. The height of the arrow is usually meant to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead.

  
  In mathematical analysis, the Dirac delta function (or δ distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as
  
  $$\delta (x)={\begin{cases}0,&x\neq 0\\{\infty },&x=0\end{cases}}$$ (Full article...)
• 
  In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction.
  
  In technical terms, QED can be described as a very accurate way to calculate the probability of the position and movement of particles, even those massless such as photons, and the quantity depending on position (field) of those particles, and described light and matter beyond the wave-particle duality proposed by Albert Einstein in 1905. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. It is the most precise and stringently tested theory in physics. (Full article...)
• 
  In mathematics, the factorial of a non-negative integer $n$, denoted by $n!$, is the product of all positive integers less than or equal to $n$. The factorial of $n$ also equals the product of $n$ with the next smaller factorial:
  $$<br>{\begin{aligned}n!&=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 3\times 2\times 1\\<br>&=n\times (n-1)!\\<br>\end{aligned}}$$
  For example,
  $$5!=5\times 4!=5\times 4\times 3\times 2\times 1=120.$$
  The value of 0! is 1, according to the convention for an empty product.
  
  Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book Sefer Yetzirah. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of $n$ distinct objects: there are $n!$. In mathematical analysis, factorials are used in power series for the exponential function and other functions, and they also have applications in algebra, number theory, probability theory, and computer science. (Full article...)
• 

  

  The regular heptagon cannot be constructed using only a straightedge and compass construction; this can be proven using the field of constructible numbers.

  
  In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.
  
  The best known fields are the field of rational numbers, the field of real numbers and the field of complex numbers. Many other fields, such as fields of rational functions, algebraic function fields, algebraic number fields, and p-adic fields are commonly used and studied in mathematics, particularly in number theory and algebraic geometry. Most cryptographic protocols rely on finite fields, i.e., fields with finitely many elements. (Full article...)
• 
  In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are order-isomorphic. For instance, Minkowski's question-mark function produces an isomorphism (a one-to-one order-preserving correspondence) between the numerical ordering of the rational numbers and the numerical ordering of the dyadic rationals.
  
  The theorem is named after Georg Cantor, who first published it in 1895, using it to characterize the (uncountable) ordering on the real numbers. It can be proved by a back-and-forth method that is also sometimes attributed to Cantor but was actually published later, by Felix Hausdorff. The same back-and-forth method also proves that countable dense unbounded orders are highly symmetric, and can be applied to other kinds of structures. However, Cantor's original proof only used the "going forth" half of this method. In terms of model theory, the isomorphism theorem can be expressed by saying that the first-order theory of unbounded dense linear orders is countably categorical, meaning that it has only one countable model, up to logical equivalence. (Full article...)
• 

  

  The logo of the International Mathematical Olympiad

  
  
  The International Mathematical Olympiad (IMO) is a mathematical olympiad for pre-university students, and is the oldest of the International Science Olympiads. It is “the most prestigious” mathematical competition in the world. The first IMO was held in Romania in 1959. It has since been held annually, except in 1980. More than 100 countries participate. Each country sends a team of up to six students, plus one team leader, one deputy leader, and observers.
  
  The content ranges from extremely difficult algebra and pre-calculus problems to problems in branches of mathematics not conventionally covered in secondary or high school and often not at university level either, such as projective and complex geometry, functional equations, combinatorics, and well-grounded number theory, of which extensive knowledge of theorems is required. Calculus, though allowed in solutions, is never required, as there is a principle that anyone with a basic understanding of mathematics should understand the problems, even if the solutions require a great deal more knowledge. Supporters of this principle claim that this allows more universality and creates an incentive to find elegant, deceptively simple-looking problems which nevertheless require a certain level of ingenuity, often times a great deal of ingenuity to net all points for a given IMO problem. (Full article...)
• 
  
  

  

  Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden

  
  Christiaan Huygens, Lord of Zeelhem, FRS (/ˈhaɪɡənz/ HY-gənz, US also /ˈhɔɪɡənz/ HOY-gənz; Dutch: [ˈkrɪstijaːn ˈɦœyɣə(n)s] ; also spelled Huyghens; Latin: Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.
  
  Huygens first identified the correct laws of elastic collision in his work De Motu Corporum ex Percussione, completed in 1656 but published posthumously in 1703. In 1659, Huygens derived geometrically the formula in classical mechanics for the centrifugal force in his work De vi Centrifuga, a decade before Newton. In optics, he is best known for his wave theory of light, which he described in his Traité de la Lumière (1690). His theory of light was initially rejected in favour of Newton's corpuscular theory of light, until Augustin-Jean Fresnel adapted Huygens's principle to give a complete explanation of the rectilinear propagation and diffraction effects of light in 1821. Today this principle is known as the Huygens–Fresnel principle. (Full article...)
• 
  Hypatia (born c. 350–370 - March 415 AD) was a Neoplatonist philosopher, astronomer, and mathematician who lived in Alexandria, Egypt, then part of the Eastern Roman Empire. She was a prominent thinker in Alexandria where she taught philosophy and astronomy. Although preceded by Pandrosion, another Alexandrian female mathematician, she is the first female mathematician whose life is reasonably well recorded. Hypatia was renowned in her own lifetime as a great teacher and a wise counselor. She wrote a commentary on Diophantus's thirteen-volume Arithmetica, which may survive in part, having been interpolated into Diophantus's original text, and another commentary on Apollonius of Perga's treatise on conic sections, which has not survived. Many modern scholars also believe that Hypatia may have edited the surviving text of Ptolemy's Almagest, based on the title of her father Theon's commentary on Book III of the Almagest.
  
  Hypatia constructed astrolabes and hydrometers, but did not invent either of these, which were both in use long before she was born. She was tolerant toward Christians and taught many Christian students, including Synesius, the future bishop of Ptolemais. Ancient sources record that Hypatia was widely beloved by pagans and Christians alike and that she established great influence with the political elite in Alexandria. Toward the end of her life, Hypatia advised Orestes, the Roman prefect of Alexandria, who was in the midst of a political feud with Cyril, the bishop of Alexandria. Rumors spread accusing her of preventing Orestes from reconciling with Cyril and, in March 415 AD, she was murdered by a mob of Christians led by a lector named Peter. (Full article...)
• 
  
  

  

  A 1933 portrait of Whittaker by Arthur Trevor Haddon titled Sir Edmund Taylor Whittaker

  
  Sir Edmund Taylor Whittaker FRS FRSE (24 October 1873 – 24 March 1956) was a British mathematician, physicist, and historian of science. Whittaker was a leading mathematical scholar of the early 20th century who contributed widely to applied mathematics and was renowned for his research in mathematical physics and numerical analysis, including the theory of special functions, along with his contributions to astronomy, celestial mechanics, the history of physics, and digital signal processing.
  
  Among the most influential publications in Whittaker's bibliography, he authored several popular reference works in mathematics, physics, and the history of science, including A Course of Modern Analysis (better known as Whittaker and Watson), Analytical Dynamics of Particles and Rigid Bodies, and A History of the Theories of Aether and Electricity. Whittaker is also remembered for his role in the relativity priority dispute, as he credited Henri Poincaré and Hendrik Lorentz with developing special relativity in the second volume of his History, a dispute which has lasted several decades, though scientific consensus has remained with Einstein. Whittaker served as the Royal Astronomer of Ireland early in his career, a position he held from 1906 through 1912, before moving on to the chair of mathematics at the University of Edinburgh for the next three decades and, towards the end of his career, received the Copley Medal and was knighted. The School of Mathematics of the University of Edinburgh holds The Whittaker Colloquium, a yearly lecture, in his honour and the Edinburgh Mathematical Society promotes an outstanding young Scottish mathematician once every four years with the Sir Edmund Whittaker Memorial Prize, also given in his honour. (Full article...)
• 

  

  Partition of a directed graph into a minimum feedback arc set (red dashed edges) and a maximum acyclic subgraph (blue solid edges)

  
  In graph theory and graph algorithms, a feedback arc set or feedback edge set in a directed graph is a subset of the edges of the graph that contains at least one edge out of every cycle in the graph. Removing these edges from the graph breaks all of the cycles, producing an acyclic subgraph of the given graph, often called a directed acyclic graph. A feedback arc set with the fewest possible edges is a minimum feedback arc set and its removal leaves a maximum acyclic subgraph; weighted versions of these optimization problems are also used. If a feedback arc set is minimal, meaning that removing any edge from it produces a subset that is not a feedback arc set, then it has an additional property: reversing all of its edges, rather than removing them, produces a directed acyclic graph.
  
  Feedback arc sets have applications in circuit analysis, chemical engineering, deadlock resolution, ranked voting, ranking competitors in sporting events, mathematical psychology, ethology, and graph drawing. Finding minimum feedback arc sets and maximum acyclic subgraphs is NP-hard; it can be solved exactly in exponential time, or in fixed-parameter tractable time. In polynomial time, the minimum feedback arc set can be approximated to within a polylogarithmic approximation ratio, and maximum acyclic subgraphs can be approximated to within a constant factor. Both are hard to approximate closer than some constant factor, an inapproximability result that can be strengthened under the unique games conjecture. For tournament graphs, the minimum feedback arc set can be approximated more accurately, and for planar graphs both problems can be solved exactly in polynomial time. (Full article...)
• 
  
  

  

  

  Two symmetric orthographic projections

  
  In geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram. That is, every three intersecting face planes of the icosahedral core intersect either on a vertex of this polyhedron or inside of it. It was studied by Max Brückner after the discovery of Kepler–Poinsot polyhedron. It can be viewed as an irregular, simple, and star polyhedron. (Full article...)

Did you know (auto-generated) –

• ... that mathematician Daniel Larsen was the youngest contributor to the New York Times crossword puzzle?
• ... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
• ... that owner Matthew Benham influenced both Brentford FC in the UK and FC Midtjylland in Denmark to use mathematical modelling to recruit undervalued football players?
• ... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
• ... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?
• ... that despite published scholarship to the contrary, Andrew Planta neither received a doctorate nor taught mathematics at Erlangen?
• ... that the discovery of Descartes' theorem in geometry came from a too-difficult mathematics problem posed to a princess?
• ... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?

More did you know –

Did you know...

• ...that every natural number can be written as the sum of four squares?
• ...that the largest known prime number is nearly 25 million digits long?
• ...that the set of rational numbers is equal in size to the set of integers; that is, they can be put in one-to-one correspondence?
• ...that there are precisely six convex regular polytopes in four dimensions? These are analogs of the five Platonic solids known to the ancient Greeks.
• ...that it is unknown whether π and e are algebraically independent?
• ...that a nonconvex polygon with three convex vertices is called a pseudotriangle?
• ...that it is possible for a three-dimensional figure to have a finite volume but infinite surface area, such as Gabriel's Horn?

Selected article –

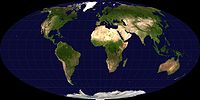An example of a map projection: the area-preserving Mollweide projection of the earth. Image credit: NASA

A map projection is any method used in cartography (mapmaking) to represent the dimensional surface of the earth or other bodies. The term "projection" here refers to any function defined on the earth's surface and with values on the plane, and not necessarily a geometric projection.

Flat maps could not exist without map projections, because a sphere cannot be laid flat over a plane without distortions. One can see this mathematically as a consequence of Gauss's Theorema Egregium. Flat maps can be more useful than globes in many situations: they are more compact and easier to store; they readily accommodate an enormous range of scales; they are viewed easily on computer displays; they can facilitate measuring properties of the terrain being mapped; they can show larger portions of the earth's surface at once; and they are cheaper to produce and transport. These useful traits of flat maps motivate the development of map projections. (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Works about mathematics

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

FL-Class Polyhedra articles

History of mathematics

Mathematical notation

Mathematical science occupations

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals