Luminance
This article needs additional citations for verification. (April 2023) |

Luminance is a photometric measure of the luminous intensity per unit area of light travelling in a given direction.[1] It describes the amount of light that passes through, is emitted from, or is reflected from a particular area, and falls within a given solid angle.
The procedure for conversion from spectral radiance to luminance is standardized by the CIE and ISO.[2]
Brightness is the term for the subjective impression of the objective luminance measurement standard (see Objectivity (science) § Objectivity in measurement for the importance of this contrast).
The SI unit for luminance is candela per square metre (cd/m2). A non-SI term for the same unit is the nit. The unit in the Centimetre–gram–second system of units (CGS) (which predated the SI system) is the stilb, which is equal to one candela per square centimetre or 10 kcd/m2.
Description
[edit]Luminance is often used to characterize emission or reflection from flat, diffuse surfaces. Luminance levels indicate how much luminous power could be detected by the human eye looking at a particular surface from a particular angle of view. Luminance is thus an indicator of how bright the surface will appear. In this case, the solid angle of interest is the solid angle subtended by the eye's pupil.
Luminance is used in the video industry to characterize the brightness of displays. A typical computer display emits between 50 and 300 cd/m2. The sun has a luminance of about 1.6×109 cd/m2 at noon.[3]
Luminance is invariant in geometric optics.[4] This means that for an ideal optical system, the luminance at the output is the same as the input luminance.
For real, passive optical systems, the output luminance is at most equal to the input. As an example, if one uses a lens to form an image that is smaller than the source object, the luminous power is concentrated into a smaller area, meaning that the illuminance is higher at the image. The light at the image plane, however, fills a larger solid angle so the luminance comes out to be the same assuming there is no loss at the lens. The image can never be "brighter" than the source.
Health effects
[edit]Retinal damage can occur when the eye is exposed to high luminance. Damage can occur because of local heating of the retina. Photochemical effects can also cause damage, especially at short wavelengths.[5]
The IEC 60825 series gives guidance on safety relating to exposure of the eye to lasers, which are high luminance sources. The IEC 62471 series gives guidance for evaluating the photobiological safety of lamps and lamp systems including luminaires. Specifically it specifies the exposure limits, reference measurement technique and classification scheme for the evaluation and control of photobiological hazards from all electrically powered incoherent broadband sources of optical radiation, including LEDs but excluding lasers, in the wavelength range from 200 nm through 3000 nm. This standard was prepared as Standard CIE S 009:2002 by the International Commission on Illumination.
Luminance meter
[edit]A luminance meter is a device used in photometry that can measure the luminance in a particular direction and with a particular solid angle. The simplest devices measure the luminance in a single direction while imaging luminance meters measure luminance in a way similar to the way a digital camera records color images.[6]
Formulation
[edit]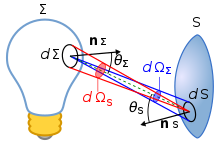
The luminance of a specified point of a light source, in a specified direction, is defined by the mixed partial derivative where
- Lv is the luminance (cd/m2);
- d2Φv is the luminous flux (lm) leaving the area dΣ in any direction contained inside the solid angle dΩΣ;
- dΣ is an infinitesimal area (m2) of the source containing the specified point;
- dΩΣ is an infinitesimal solid angle (sr) containing the specified direction; and
- θΣ is the angle between the normal nΣ to the surface dΣ and the specified direction.[7]
If light travels through a lossless medium, the luminance does not change along a given light ray. As the ray crosses an arbitrary surface S, the luminance is given by where
- dS is the infinitesimal area of S seen from the source inside the solid angle dΩΣ;
- dΩS is the infinitesimal solid angle subtended by dΣ as seen from dS; and
- θS is the angle between the normal nS to dS and the direction of the light.
More generally, the luminance along a light ray can be defined as where
- dG is the etendue of an infinitesimally narrow beam containing the specified ray;
- dΦv is the luminous flux carried by this beam; and
- n is the index of refraction of the medium.
Relation to illuminance
[edit]
The luminance of a reflecting surface is related to the illuminance it receives: where the integral covers all the directions of emission ΩΣ,
- Mv is the surface's luminous exitance;
- Ev is the received illuminance; and
- R is the reflectance.
In the case of a perfectly diffuse reflector (also called a Lambertian reflector), the luminance is isotropic, per Lambert's cosine law. Then the relationship is simply
Units
[edit]A variety of units have been used for luminance, besides the candela per square metre. Luminance is essentially the same as surface brightness, the term used in astronomy. This is measured with a logarithmic scale, magnitudes per square arcsecond (MPSAS).
| cd/m2 (SI unit) ≡ nit ≡ lm/m2/sr |
stilb (sb) (CGS unit) ≡ cd/cm2 |
apostilb (asb) ≡ blondel |
bril | skot (sk) | lambert (L) | foot-lambert (fL) = 1 ⁄ π cd/ft2 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 cd/m2 | = | 1 | 10−4 | π ≈ 3.142 |
107 π ≈ 3.142×107 |
103 π ≈ 3.142×103 |
10−4 π ≈ 3.142×10−4 |
0.30482 π ≈ 0.2919 | ||
| 1 sb | = | 104 | 1 | 104 π ≈ 3.142×104 |
1011 π ≈ 3.142×1011 |
107 π ≈ 3.142×107 |
π ≈ 3.142 |
30.482 π ≈ 2919 | ||
| 1 asb | = | 1 ⁄ π ≈ 0.3183 |
10−4 ⁄ π ≈ 3.183×10−5 |
1 | 107 | 103 | 10−4 | 0.30482 ≈ 0.09290 | ||
| 1 bril | = | 10−7 ⁄ π ≈ 3.183×10−8 |
10−11 ⁄ π ≈ 3.183×10−12 |
10−7 | 1 | 10−4 | 10−11 | 0.30482×10−7 ≈ 9.290×10−9 | ||
| 1 sk | = | 10−3 ⁄ π ≈ 3.183×10−4 |
10−7 ⁄ π ≈ 3.183×10−8 |
10−3 | 104 | 1 | 10−7 | 0.30482×10−3 ≈ 9.290×10−5 | ||
| 1 L | = | 104 ⁄ π ≈ 3183 |
1 ⁄ π ≈ 0.3183 |
104 | 1011 | 107 | 1 | 0.30482×104 ≈ 929.0 | ||
| 1 fL | = | 1 ⁄ 0.30482 ⁄ π ≈ 3.426 |
1 ⁄ 30.482 ⁄ π ≈ 3.426×10−4 |
1 ⁄ 0.30482 ≈ 10.76 |
107 ⁄ 0.30482 ≈ 1.076×108 |
103 ⁄ 0.30482 ≈ 1.076×104 |
10−4 ⁄ 0.30482 ≈ 1.076×10−3 |
1 | ||
See also
[edit]- Relative luminance
- Orders of magnitude (luminance)
- Diffuse reflection
- Etendue
- Exposure value § EV as a measure of luminance and illuminance
- Lambertian reflectance
- Lightness (color)
- Luma, the representation of luminance in a video monitor
- Lumen (unit)
- Radiance, radiometric quantity analogous to luminance
- Brightness, the subjective impression of luminance
- Glare (vision)
Table of SI light-related units
[edit]
| Quantity | Unit | Dimension [nb 1] |
Notes | ||
|---|---|---|---|---|---|
| Name | Symbol[nb 2] | Name | Symbol | ||
| Luminous energy | Qv[nb 3] | lumen second | lm⋅s | T⋅J | The lumen second is sometimes called the talbot. |
| Luminous flux, luminous power | Φv[nb 3] | lumen (= candela steradian) | lm (= cd⋅sr) | J | Luminous energy per unit time |
| Luminous intensity | Iv | candela (= lumen per steradian) | cd (= lm/sr) | J | Luminous flux per unit solid angle |
| Luminance | Lv | candela per square metre | cd/m2 (= lm/(sr⋅m2)) | L−2⋅J | Luminous flux per unit solid angle per unit projected source area. The candela per square metre is sometimes called the nit. |
| Illuminance | Ev | lux (= lumen per square metre) | lx (= lm/m2) | L−2⋅J | Luminous flux incident on a surface |
| Luminous exitance, luminous emittance | Mv | lumen per square metre | lm/m2 | L−2⋅J | Luminous flux emitted from a surface |
| Luminous exposure | Hv | lux second | lx⋅s | L−2⋅T⋅J | Time-integrated illuminance |
| Luminous energy density | ωv | lumen second per cubic metre | lm⋅s/m3 | L−3⋅T⋅J | |
| Luminous efficacy (of radiation) | K | lumen per watt | lm/W | M−1⋅L−2⋅T3⋅J | Ratio of luminous flux to radiant flux |
| Luminous efficacy (of a source) | η[nb 3] | lumen per watt | lm/W | M−1⋅L−2⋅T3⋅J | Ratio of luminous flux to power consumption |
| Luminous efficiency, luminous coefficient | V | 1 | Luminous efficacy normalized by the maximum possible efficacy | ||
| See also: | |||||
- ^ The symbols in this column denote dimensions; "L", "T" and "J" are for length, time and luminous intensity respectively, not the symbols for the units litre, tesla and joule.
- ^ Standards organizations recommend that photometric quantities be denoted with a subscript "v" (for "visual") to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967
- ^ a b c Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ for luminous efficacy of a source.
References
[edit]- ^ "luminance, 17-21-050". CIE S 017:2020 ILV: International Lighting Vocabulary, 2nd edition. CIE - International Commission on Illumination. 2020. Retrieved 20 April 2023.
- ^ ISO/CIE 23539:2023 CIE TC 2-93 Photometry — The CIE system of physical photometry. ISO/CIE. 2023. doi:10.25039/IS0.CIE.23539.2023.
- ^ "Luminance". Lighting Design Glossary. Retrieved Apr 13, 2009.
- ^ Dörband, Bernd; Gross, Herbert; Müller, Henriette (2012). Gross, Herbert (ed.). Handbook of Optical Systems. Vol. 5, Metrology of Optical Components and Systems. Wiley. p. 326. ISBN 978-3-527-40381-3.
- ^ IEC 60825-1:2014 Safety of laser products - Part 1: Equipment classification and requirements (in English, French, and Spanish) (3rd ed.). International Electrotechnical Commission. 2014-05-15. p. 220. - TC 76 - Optical radiation safety and laser equipment
- ^ "e-ILV : Luminance meter". CIE. Archived from the original on 16 September 2017. Retrieved 20 February 2013.
- ^ Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. p. 679. ISBN 978-1482206739. Archived from the original on 2016-02-18.
External links
[edit]- A Kodak guide to Estimating Luminance and Illuminance using a camera's exposure meter. Also available in PDF form.
- Autodesk Design Academy Measuring Light Levels





